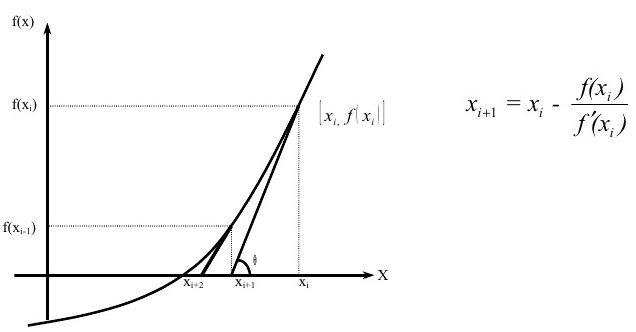
Newton-Raphson metodu, sayısal analizde, eşitlik köklerinin bulunmasında en yaygın kullanılan metotlardan birisidir. Başlangıç için tahmini bir kök değeri seçilerek, yapılan iterasyon sonucu gerçek kök değerine oldukça yakın bir değere ulaşılır.

Newton-Raphson metodunun C# dilinde yazılmış kaynak kodu yer almaktadır.

public class NewtonRaphson
{
    public uint MaxIteration { get; set; } = 50;
    public double Epsilon { get; set; } = 0.000001;

    public double Solve(Func<double, double> f, Func<double, double> df, double initialGuess)
    {
        var xn = initialGuess;

        for (var i = 0; i < this.MaxIteration; i++)
        {
            var xn1 = xn - f.Invoke(xn) / df.Invoke(xn);

            if (Math.Abs(xn - xn1) < this.Epsilon)
            {
                return xn1;
            }

            xn = xn1;
        }

        return xn;
    }
}

Örneğin f(x) = x^2 - 2 fonksiyonun köklerini bulmak için, metodu aşağıdaki şekilde çağırabiliriz. Tahmini kök değeri olarak 1 seçilmiştir.

var solver = new NewtonRaphson();
var root = solver.Solve(x => x * x - 2, x => 2 * x, 1);

Benzer şekilde, f(x) = x - Cos(x) fonksiyonun köklerini bulmak için ise, metodu aşağıdaki şekilde çağırabiliriz. f(x) = 1 + Sin(x) fonksiyonun türevidir.

var solver = new NewtonRaphson();
var root = solver.Solve(x => x - Math.Cos(x), x => 1 + Math.Sin(x), 2);